Question

James creates the table shown to represent the function ƒ(x) = x2 + 8x + 12. Determine the zero(s) of the function.

Answer 1

I believe that the zeros would be -2 and -6, assuming that the first 2 that you wrote in the equation is supposed to be a power to the x.

Answer 2

x = -6 and -2 are the zero(s) of the function

Explanation:

To find the zero(s) of the function f(x).

Given the function:

`f(x) = x^2+8x+12`

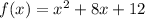
Set f(x) = 0

then;

`x^2+8x+12 = 0`

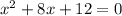
Now factorize the equation as:

`x^2+6x+2x+12 = 0`

⇒
`x(x+6)+2(x+6) = 0`

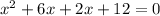
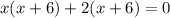
take (x+6) common we have;

`(x+6)(x+2)=0`

By zero product property we have;

⇒x+6 = 0 or x+2 = 0

⇒x = -6 or x = -2

therefore, the zero(s) of the function are -6 and -2