Question

How can I find the radious of convergence and the interval of convergence for this series

Answer 1

The ratio or root tests are the usual go-to methods.

By the ratio test, the series will converge if


`\displaystyle\lim_(n\to\infty)\left|((n+1)!(4x-1)^(n+1))/(n!(4x-1)^n)\right|<1`

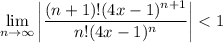
The limit reduces to


`|4x-1|\displaystyle\lim_(n\to\infty)|n+1|=\infty>1`

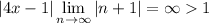
which means the series diverges everywhere except the point
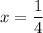
`x=\frac14`, where the series evaluates to 0. So because the series diverges, the interval of convergence is a single point, and so the radius of convergence is 0.