Question

A grasshopper jumps at a 65.0 degree angle at 5.42m/s. At what time does it reach its maximum height?

Answer 1

When the grasshoppers vertical velocity is exactly zero.
v = -g•t + v0.
v: vertical part of velocity. Is zero at maximum height.
g: 9.81
t: time you are looking for
v0: initial vertical velocity
Find the vertical part of the initial velocity, by using the angle at which the grasshopper jumps.

Answer 2

A grasshopper reached the maximum height 1.23 m.

Step-by-step explanation:

Given that,

Velocity = 5.42 m/s

Angle = 65.0°

We need to calculate the maximum height

Using formula of maximum height

`y_(max)=(v^2\sin^2\theta)/(2g)`

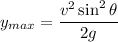
Where, v = 5.42 m/s

g = acceleration due to gravity

`\theta` =Angle

Put the value into the formula

`y_(max)=(5.42^2*\sin^2(65.0))/(2*9.8)`

`y_(max)=1.23\ m`

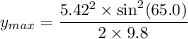
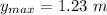
Hence, A grasshopper reached the maximum height 1.23 m.