Question

Consider the level surface given by

x2−y2+z2=2. Draw a picture for the following:
1. Slice for y=2
2. Slice for x=1
3. Slice for y=0
4. Slice for x=2 ...?

Answer 1

`x^2-y^2+z^2=2`

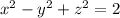
If
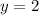
`y=2`, then you get
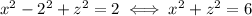
`x^2-2^2+z^2=2\iff x^2+z^2=6` which is a circle in the x-z plane with radius
`\sqrt6`.

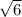
If
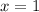
`x=1`, then you get
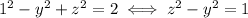
`1^2-y^2+z^2=2\iff z^2-y^2=1` which is a hyperbola in the y-z plane.

If
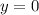
`y=0`, you get another circle in the x-z plane defined by
`x^2+z^2=2`, this time with radius
`\sqrt2`.

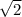
If
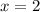
`x=2`, then
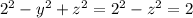
`2^2-y^2+z^2=2\iffy^2-z^2=2`, another hyperbola in the y-z plane with branches perpendicular to the case where
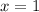
`x=1`.