If

satisfies the ODE
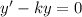
, then
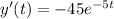
and substituting into the ODE gives
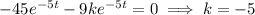
so that the ODE is
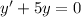
.
I'm assuming that you're also supposed to determine the initial value
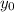
given this ODE. You have

Given
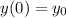
, you have
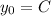
but since you already know that
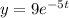
, it follows that
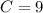
, and in turn that
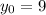
.