Question

Write the equation of the function shown below. Identify domain and range.

Answer 1

The function can be split in 2 straight lines: the first one from x = 2 to the left, and the other one from the same point to the right.

Now, a straight line equation is of the form

`ax+m`

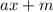
Where a is the slope and m is the y-intercept.

"Left" line:

- m (y-intercept):

To find it we need to see where the line cross (intercepts) the y-axis. From the figure we can see that m = -2.

- a (slope):

To calculate the slope, we can use the following equation:

`a=(\Delta y)/(\Delta x)`

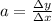
Where, chossing 2 points in the line, we have:

`\begin{gathered} \Delta y=how\text{ much do we move up or down between the 2 points} \\ \Delta x=\text{ how much do we move to the right betw}en\text{ the 2 points} \end{gathered}`

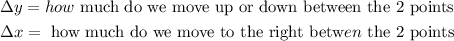
Look that for x we have to move to the right. Let's see a drawing:

In our case, we can take the points (0, -2) and (2, 4), so, we have:

`a=(\Delta y)/(\Delta x)=(4-(-2))/(2-0)=(6)/(2)=3`

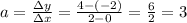
So, we have the equation for the "left" line:

`3x-2`

-"Right" line:

- m (y-intercept):

In this case we can not see where the line cross (intercepts) the y-axis. Let's leave this for latter.

- a (slope):

As we did before, we can pick to points on the line, like (3, 1) and (2, 4).

`a=(\Delta y)/(\Delta x)=(1-4)/(3-2)=(-3)/(1)=-3`

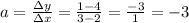
- m (y-intercept) continues:

We now know that the equation for this line is:

`-3x+m`

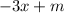
To find m, we can pick one single point and solve for that variable. For example, taking the point (2,4), we have:

`\begin{gathered} y=ax+m \\ y=-3x+m \\ 4=-3\cdot(2)+m \\ 4=-6+m \\ 4+6=m \\ 10=m \end{gathered}`

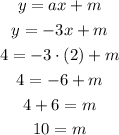
And so, for the right line, we have:

`-3x+10`

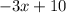
Finally, the equation of the function can be written as:

`f(x)=\begin{cases}3x-2\text{ if x }\leq\text{ 2} \\ -3x+10\text{ if x }\ge\text{ 2}\end{cases}`

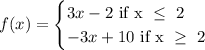
Now, the domain of the function is the set of points (or numbers) for which the function has values. The set of departure. In this case, all the numbers can be "trasnformed" or mapped with this function, so the domain is all the numbers, the set of real numbers, R: