Question

Identify the range y=3^x

Answer 1

The range of the function is:

`\mathrm{Range\:of\:}3^x:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)>0\:\\ \:\mathrm{Interval\:Notation:}&\:\left(0,\:\infty \:\right)\end{bmatrix}`

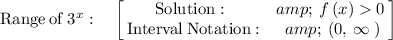
Please also check the attached graph.

Explanation:

We also know that range is the set of values of the dependent variable for which a function is defined.

In other words,

Range refers to all the possible sets of output values on the y-axis.

It means the set of all the y-coordinates of the given points or ordered pairs on a graph will be the range.

Given the expression

`y=3^x`

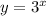
The range of an exponential function of the form

`c\cdot \:n^(ax+b)+k\:\mathrm{is}\:\:f\left(x\right)>k`

`k=0`

`f\left(x\right)>0`

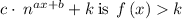
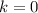
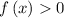
Therefore, the range of the function is:

`\mathrm{Range\:of\:}3^x:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)>0\:\\ \:\mathrm{Interval\:Notation:}&\:\left(0,\:\infty \:\right)\end{bmatrix}`

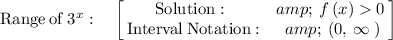
Please also check the attached graph.