Question

5

4
2
1
O
3
4
5
A
Which equation best represents the line? (4 points)
Oy - 3x - 1
Oy - 3x + 1

Answer 1

The equation best represents the line is:

• y = 3x-1

Explanation:

The slope-intercept form of the line equation

y = mx+b

where

• m is the slope

• b is the y-intercept

Taking the two points

• (0, -1)

• (1, 2)

Determining the slope between the points (0, -1) and (1, 2)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(0,\:-1\right),\:\left(x_2,\:y_2\right)=\left(1,\:2\right)`

`m=(2-\left(-1\right))/(1-0)`

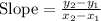
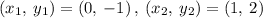
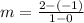
Refine

`m=3`

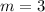
We know that the value of the y-intercept can be determined by setting x = 0 and determining the corresponding value of y.

As we are given the point (0, -1)

It means at x = 0, y = -1

Thus, the y-intercept b = -1

now substituting b = -1 and m = 3 in the slope-intercept form

y = mx+b

y = 3x + (-1)

y = 3x-1

Therefore, the equation best represents the line is:

• y = 3x-1