Question

Write the exponential function y - 45(1.085)^t in the form y = ae^kt(a) Once you have rewritten the tormula, give & accurate to at least four decimal places.K=If T is measured in years, indicate whether the exponential function is growing or decaying and find he annual and continuous growth/decay rates. The rates you determine should be positive in the case of growth or decay (by choosing decay the negative rate is implied).(b) The annual (growth/decay) rate is ___ % per yearC) The continuous (growth/decay) rate is ___ % per year

Answer 1

Step-by-step explanation

Given the exponential function:

45(1.085)^t

We have that 45=a is the initial value and 1.085 is the growth rate,

1.085 - 1 = 0.085* 100 = 8.5 % (This is the growth rate)

Let's compute the function with two values of t, as for instance, t=0 and t=1:

`f(0)=45(1.085)^0=45\cdot1=45\longrightarrow\text{ (0,45)}`
`f(1)=45\cdot(1.085)^1=48.825\text{ }\longrightarrow\text{(1,48.825)}`

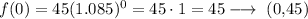
Now, the function in the form y = ae^kt will be as follows:

`y=45\cdot e^(kt)`

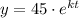
Substituting t by 1:

`y(1)=45\cdot e^k=48.825`

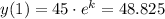
Dividing both sides by 45:

`e^k=(48.825)/(45)=1.085`

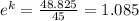
Applying ln to both sides:

`k=\ln 1.085`

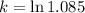
Computing the argument:

`k=0.0816`

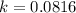
The expression will be as follows:

`(a)---\longrightarrow y=45e^(0.0816t)`

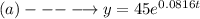
As this is a growing function, the rates are positive.

The annual growth rate is 8.5% and It's was calculated above.

Now, we need to compute the continuous rate because It's given by the value of k:

k = 0.0816 --> Multiplying by 100 --> 0.0816 * 100 = 8.16%

The continuous growth rate is 8.16%