Answer:
The hypothenuse is 10 meters long.
Explanation:
We know by defintion that a right triangle has a righ angle which is equal to 90°.
So, by given, we know that one of the acute angles is 45°, that means the other acute angle is also 45°, because all three internal angles must sum 180°.
Now, the given angle is

And its opposite side is
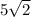 .
.
To find the hypothenuse we need to use the sin function, which relates the angle with its opposite side and the hypothenuse.

Now, we solve for
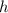
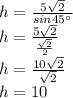
Thereofre, the hypothenuse is 10 meters long.