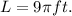Question

In a circle with a radius of 6 ft, an arc is intercepted by a central angle of 3π/2 radians.

What is the length of the arc?

2π ft

​ 3π ​ ft

​ 6π ​ ft

​ 9π ​ ft

Answer 1

9π ​ ft

Explanation:

Answer 2

Option 4 -
`L=9\pi ft.`

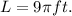
Explanation:

Given : In a circle with a radius of 6 ft, an arc is intercepted by a central angle of 3π/2 radians.

To find : What is the length of the arc?

Solution :

Length of an arc is given by:

`L=r\theta`

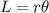
where r is the radius of the circle, r= 6 ft.

and
`\theta` is the angle in radian,
`\theta=(3\pi )/(2)`

Substitute the value given in the formula,

`L=r\theta`

`L=6* (3\pi )/(2)`

`L=3*3\pi`

`L=9\pi`

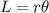
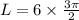
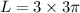
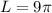
Therefore, Option 4 is correct.

The arc of length is
`L=9\pi ft.`