Answer:
The limit of the function does not exists.
Explanation:
From the graph it is noticed that the value of the function is 6 from all values of x which are less than 2. At x=2, the line y=6 has open circle. It means x=2 is not included.
For x<2

The value of the function is -3 from all values of x which are greater than 2. At x=2, the line y=-3 has open circle. It means x=2 is not included.
For x>2

The value of y is 1 at x=2, because of he close circles on (2,1).
For x=2
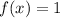
Therefore the graph represents a piecewise function, which is defined as

The limit of a function exist at a point a if the left hand limit and right hand limit are equal.
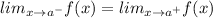
The function is broken at x=2, therefore we have to find the left and right hand limit at x=2.

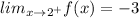
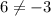
Since the left hand limit and right hand limit are not equal therefore the limit of the function does not exists.