Question

Find the four terms of the arithmetic sequence given the 13th term (a_{13}=-60) and the thirty third term (a_{33}=-160).Given terms: a_{13}=-60 and a_{33}= -160Find these terms:a_{14}= Answera_{15}= Answera_{16}= Answera_{17}= Answer

Answer 1

Given:

13th term = -60

33rd term = -160

Find:

14th, 15th, 16th, and 17th term

Solution:

For us to determine the 14 - 17th term, we need to identify the common difference in this arithmetic sequence. The formula is:

`(a_(33)-a_(13))/(33-13)`

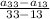
Let's plug in the values of a₃₃ and a₁₃ in the formula above.

`(-160-(-60))/(33-13)`

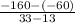
Then, solve.

`(-100)/(20)=-5`

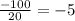
Hence, the common difference between the terms is -5.

So, the next 4 terms after a₁₃ are shown below:

`\begin{gathered} a_(14)=-65 \\ a_(15)=-70 \\ a_(16)=-75 \\ a_(17)=-80 \end{gathered}`