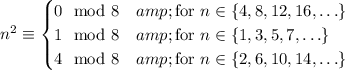Question

Show that every perfect square is congruent to 0, 1, or 4 modulo 8

Answer 1

You want to prove that


`n^2\equiv k\mod8,k\in\{0,1,4\}`

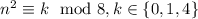
for (presumably) all integers
`n\ge1`.

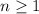
Let's consider some sub-cases.

Suppose
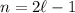
`n=2\ell-1` is odd. Then


`n^2=(2\ell-1)^2=4\ell^2-4\ell+1`

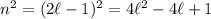
If
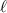
`\ell` is even, then so is
`\ell^2-\ell`, which means you can write
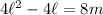
`4\ell^2-4\ell=8m` for some integer
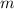
`m`, and this reduces to
`n^2\equiv1\mod8`.

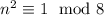
If
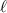
`\ell` is odd, the same thing happens; you get that
`\ell^2-\ell` is still even, so
`4\ell^2-4\ell\equiv0\mod8` and you're left again with
`n^2\equiv1\mod8`.

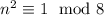
Now assume
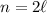
`n=2\ell` is even. Then
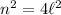
`n^2=4\ell^2`. If
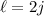
`\ell=2j` is even, then you will always be able to write


`n^2=(2\ell)^2=4\ell^2=4(2j)^2=8*2j^2\equiv0\mod8`

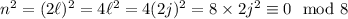
Meanwhile, if
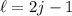
`\ell=2j-1` is odd, then


`n^2=4\ell^2=4(2j-1)^2=16j^2-16j+4\equiv4\mod8`

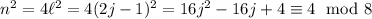
So you conclude that


`n^2\equiv\begin{cases}0\mod8&\text{for }n\in\{4,8,12,16,\ldots\}\\1\mod8&\text{for }n\in\{1,3,5,7,\ldots\}\\4\mod8&\text{for }n\in\{2,6,10,14,\ldots\}\end{cases}`