Answer:
a) 3, 6, 9, 12, 15,...,
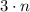 , b) 4, 7, 10, 13, 16,...,
, b) 4, 7, 10, 13, 16,...,
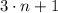 , c) Both sequences are arithmetic.
, c) Both sequences are arithmetic.
Explanation:
a) The sequence of natural numbers which are multiplied by 3 are represented by the function
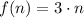 ,
,
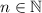 . Let see the first five elements of the sequence: 3, 6, 9, 12, 15,...
. Let see the first five elements of the sequence: 3, 6, 9, 12, 15,...
b) The sequence of natural numbers which are multiplied by 3 and added to 1 is represented by the function
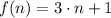 ,
,
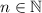 . Let see the first five elements of the sequence: 4, 7, 10, 13, 16,...
. Let see the first five elements of the sequence: 4, 7, 10, 13, 16,...
c) Both sequences since differences between consecutive elements is constant. Let prove this statement:
(i)
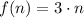
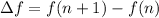
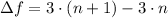
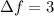
(ii)
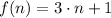
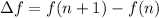
![\Delta f = [3\cdot (n+1)+1]-(3\cdot n+1)](https://img.qammunity.org/2022/formulas/mathematics/high-school/iid4n8v3dq8xgrnx1lr0vzo56z8oyti7ux.png)
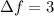
Both sequences are arithmetic.