Question

Select all of the segments that must be 9 centimeters long.

Answer 1

Given:

KM=12 cm.

KO=1+KL

`KL=(1)/(3)LM`

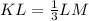
Since KM=12 cm, we can write

`\begin{gathered} KM=KL+LM \\ KM=(1)/(3)LM+LM \\ 12\text{ =}(4)/(3)LM \\ LM=(12*3)/(4) \\ LM=9 \end{gathered}`

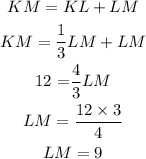
Therefore, KL can be calculated as,

`\begin{gathered} KL=(1)/(3)LM \\ =(1)/(3)*9 \\ =3 \end{gathered}`

Now, KO can be calculated as,

`\begin{gathered} KO=1+KL \\ =1+3 \\ =4 \end{gathered}`

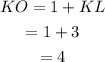
Now, using geometric property,

`KM* KL=KN* KO`

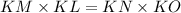
Putting the values in the above equation, KN can be calculated as,

`\begin{gathered} 12*3=KN*4 \\ KN=(12*3)/(4) \\ KN=9 \end{gathered}`

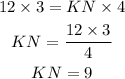
Now, ON can be calculated as,

`\begin{gathered} ON=KN-KO \\ =9-4 \\ =5 \end{gathered}`

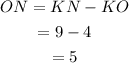
Since LM=9 is a chord longer than MN in the given circle, the length of MN is less than 9.

Therefore, the segments with length 9 are LM and KN.