Answer:
a.5
b.5
c.Yes
d.No
Step-by-step explanation:
We are given a function
a.
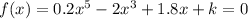
We have to find the number of real solutions when k=0
Using Discarte's rule of sign
When we go from coefficient of first term to coefficient of second term then sign changes and we go from coefficient of second term to coefficient of third term then sign again changes.
Therefore, there are two sign change hence, two positive real roots or less but even in number .
Therefore, possible value or real positive real root is 2 or 0
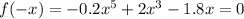
There are two times sign change.Hence, there are two negative real roots or less and even in number.
Therefore, possible values 2 or 0
When k=0
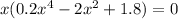
x=0
Discriminant for quadratic equation in x square
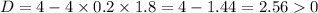
Hence, two roots are positive and two roots are negative and zero.
Number of roots of given function is 5.
b.When k= 1
Using Discarte's rule
Then there are two or less positive real roots and 3 or less negative real roots but odd in number .Therefore, negative real roots are 3 or 1
When k=1
Product of roots=-1
Sum of roots =0
When 3 or negative real roots then product of roots is also negative .But one negative root is not possible because sum of roots is zero.Hence, there are three negative real roots.
If we take no real positive roots and roots are imaginary.Imaginary roots occur in pairs. Then sum of roots can not be zero.Hence ,there are two positive real roots.Hence, there are 5 real roots when k=1
c.Yes, if we take value of k is negative then there are positive real roots can be 3 or 1 and negative real roots can be 2 or 0. .Therefore, that case can be possible .
d.No, there are no such value for which function no real solution.