Question

In two or more complete sentences, describe the transformation(s) that take place on the parent function, f(x) = log(x), to achieve the graph of g(x) = log(-2x-4) + 2.

Answer 1

Answer and explanation:

To find : Describe the transformation(s) that take place on the parent function,
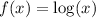`f(x) =\log(x)`, to achieve the graph of
`g(x) = \log(-2x-4) +2`

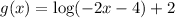
Solution :

Parent function:
`f(x) =\log(x)`

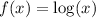
Transformation function:
`g(x) = \log(-2x-4) +2`

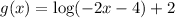
Re-write the transformed function by taking -2 common,

`g(x) =\log(-2(x+2))+2`

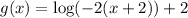
Step 1 - Shift 2 unit left i.e, f(x)→f(x+b) shifting left by b unit in parent function,

`f(x)=\log(x+2)`

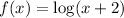
Step 2 - Flip the graph about y-axis i.e, f(x)→ -f(x)

`f(x)=\log[-(x+2)]`

Step 3 - Stretch horizontally by factor 2 i.e, f(x)→f(bx) stretch horizontally by b unit

`f(x)=\log[-2(x+2)]`

Step 4 - Shift vertically up by 2 units i.e, f(x)→f(x)+b shifting vertically by b unit

`f(x) =\log(-2(x+2))+2=g(x)`

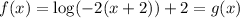
In four steps the transformation is done.

Answer 2

Shift 2 unit left

Flip the graph about y-axis

Stretch horizontally by factor 2

Shift vertically up by 2 units

Explanation:

Given:

Parent function:
`f(x)=\log x`

Transformation function:
`f(x)=\log(-2x-4)+2`

Take -2 common from transform function f(x)

`f(x)=\log[-2(x+2)]+2`

Now we see the step-by-step translation

`f(x)=\log x`

Shift 2 unit left ( x → x+2 )

`f(x)=\log(x+2)`

Flip the graph about y-axis ( (x+2) → - (x+2) )

`f(x)=\log[-(x+2)]`

Stretch horizontally by factor 2 [ -x(x+2) → -2(x+2) ]

`f(x)=\log[-2(x+2)]`

Shift vertically up by 2 units [ f(x) → f(x) + 2 ]

`f(x)=\log[-2(x+2)]+2`

Simplify the function:

`f(x)=\log(-2x-4)+2`

Hence, Using four step of transformation to get new function
`f(x)=\log(-2x-4)+2`