Question

A 1.47-newton baseball is dropped from a height of 10.0 meters and falls through the air to the ground. The kinetic energy of the ball is 12.0 joules the instant before the ball strikes the ground. What is the maximum amount of mechanical energy converted to internal energy during the fall?

Answer 1

See the explanation below.

Step-by-step explanation:

First, we must determine the mass of the baseball, we know that the weight of a body is defined as the product of mass by gravity.

`w=m*g`

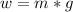
where:

w = weight = 1.47[N]

m = mass [kg]

g = gravity acceleration = 9.81 [m/s²]

Now replacing:

`m=w/g\\m = 1.47/9.81\\m = 0.149[kg]`

We now know that kinetic energy is converted to potential energy as the ball descends. By means of the following equation, we can determine the potential energy when the baseball is 10 meters high.

`E_(pot)=m*g*h\\`

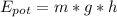
where:

Epot = potential energy [J]

m = mass = 0.149[kg]

g = gravity acceleration = 9.81 [m/s²]

h = elevation = 10 [m]

Now replacing:

`E_(pot)=0.149*9.81*10\\E_(pot)=14.7[J]`

In theory, this same energy must be converted to kinetic energy just before the ball hits the floor. But we see that we only have 12 [J] of kinetic energy.

That is to say, that of the 14 [J] that were had as potential energy (mechanical energy) 2 [J] was converted to internal energy, and the rest was converted to kinetic energy (mechanical energy)

`E_(int)=14-12\\E_(int)=2[J]`

Note: Potential, kinetic and elastic energies are forms of mechanical energy.