Question

The image of F(-5,-9) after translating along <4, 6 > and then translating along < 3, 5> is? F’(?,?)

Answer 1

Answer: (2, 2)

==============================================

Step-by-step explanation:

The phrasing "translated along <4,6>" is another way of saying "shift 4 to the right, shift 6 up"

In general, "translated along <m,n>" is the same as writing
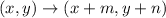`(x,y) \to (x+m, y+n)`. If m is positive, then we shift m units to the right. If m is negative, then we shift to the left. The same story happens with the n, but we focus on the y coordinate.

-------------

With all that in mind, starting at F(-5,-9) and translating along <4,6> has us arrive at (-1, -3). Add 4 to the x coordinate and add 6 to the y coordinate.

We can say

`(x,y) \to (x+4,y+6)\\\\(-5,-9) \to (-5+4,-9+6)\\\\(-5,-9) \to (-1,-3)\\\\`

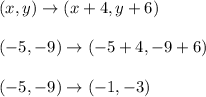
Showing that (-5,-9) moves to (-1,-3)

This is after the first translation, but there's a second translation.

We'll apply the same idea, but different numbers this time

`(x,y) \to (x+3,y+5)\\\\(-1,-3) \to (-1+3,-3+5)\\\\(-1,-3) \to (2,2)\\\\`

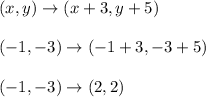
So (-1,-3) moves to (2,2)

Overall we have

• (-5,-9) move to (-1,-3) after the first translation
• (-1,-3) move to (2,2) after the second translation

Therefore, the original point ends up at (2,2) which is the final answer

--------------

Extra info:

A nice shortcut is that the vectors <4,6> and <3,5> can be added to get <4+3,6+5> = <7,11>. So overall, we're shifting 7 units to the right and 11 units up when we combine the two translation vectors.