There are six digits to choose from, but you're only taking three at a time, so the number of such numbers is
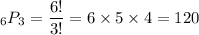
The first and last digits can only be even if the number takes the one of the forms "2 _ 8" or "8 _ 2". The middle number can be any of the remaining four, so there is a total of eight such numbers.
This means the probability of getting a number beginning and ending with an even digits is
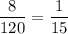
.