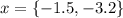Question

I need to round to the narest tenth

Answer 1

We are given the following equation

`3x^2+7x+14=-7x`

Let us solve the equation for x.

First of all, rearrange the equation so that all the terms are on the left side of the equation

`\begin{gathered} 3x^2+7x+14=-7x \\ 3x^2+7x+7x+14=0 \\ 3x^2+14x+14=0 \end{gathered}`

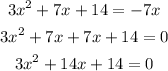
Recall that the standard form of a quadratic equation is given by

`ax^2+bx+c=0`

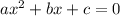
Comparing the given equation with the standard form, the coefficients are

a = 3

b = 14

c = 14

Recall that the quadratic formula is given by

`x=(-b\pm√(b^2-4ac))/(2a)`

Let us substitute the values of coefficients and simplify

`\begin{gathered} x=\frac{-14\pm\sqrt[]{14^2-4(3)(14)}}{2(3)} \\ x=\frac{-14\pm\sqrt[]{196^{}-168}}{6} \\ x=\frac{-14\pm\sqrt[]{28}}{6} \\ x=\frac{-14+\sqrt[]{28}}{6},\: \: x=\frac{-14-\sqrt[]{28}}{6} \\ x=-1.5,\: \: x=-3.2 \end{gathered}`

Therefore, the solution of the equation is

`x=\mleft\lbrace-1.5,-3.2\mright\rbrace`