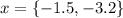We are given the following equation
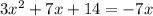
Let us solve the equation for x.
First of all, rearrange the equation so that all the terms are on the left side of the equation
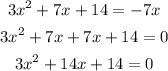
Recall that the standard form of a quadratic equation is given by
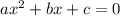
Comparing the given equation with the standard form, the coefficients are
a = 3
b = 14
c = 14
Recall that the quadratic formula is given by
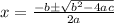
Let us substitute the values of coefficients and simplify
![\begin{gathered} x=\frac{-14\pm\sqrt[]{14^2-4(3)(14)}}{2(3)} \\ x=\frac{-14\pm\sqrt[]{196^{}-168}}{6} \\ x=\frac{-14\pm\sqrt[]{28}}{6} \\ x=\frac{-14+\sqrt[]{28}}{6},\: \: x=\frac{-14-\sqrt[]{28}}{6} \\ x=-1.5,\: \: x=-3.2 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/mmowki2k30p995qd6hik.png)
Therefore, the solution of the equation is