Question

The differential equation dy/dx=2x(4-y)

I. produces a slope field with horizontal tangents at y = 4
II. produces a slope field with horizontal tangents at x = 0
III. produces a slope field with vertical tangents at x = 0 and y = 4


which is true?
i only
ii only
i and ii
iii only

Answer 1

horizontal means dy/dx=0
vertical means that you are dividing by 0 or dy/dx is undefined



at x=0, dy/dx=0
at y=4, dy/dx=0
so the answer is I and II

answer is 3rd option

Answer 2

The correct option is 3. Statement i and ii are correct.

Explanation:

The given differential equation is

`(dy)/(dx)=2x(4-y)`

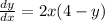
We know that
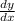`(dy)/(dx)` represents the slope of a function.

The slope of a vertical line is infinity and the slope of horizontal line is 0.

For horizontal tangents

`(dy)/(dx)=0`

`2x(4-y)=0`

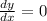
Using zero product property equation each factor equal to 0.

`2x=0\Rightarrow x=0`

`4-y=0\Rightarrow y=4`

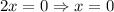
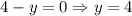
Therefore given differential equation the produces a slope field with horizontal tangents at y = 4 and at x=0. Statement i and ii are correct.