Answer:
12x-34 or -34+12x
Explanation:
We know that one dragonfruit is
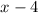 dollars. This means that one rambutan is
dollars. This means that one rambutan is
 dollars. Then, one starfruit is
dollars. Then, one starfruit is
 dollars. We want to find
dollars. We want to find
 . Distributing these three smaller expressions gives us
. Distributing these three smaller expressions gives us
 . Finally, we combine like terms, yielding
. Finally, we combine like terms, yielding
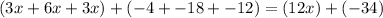 . We obtain
. We obtain
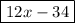 or
or
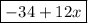 .
.
Hope this helped! :)