Answer:
Option A is correct
Vertex = (2, -7)
Explanation:
A quadratic equation is in the form of:
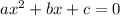 .....[1]
.....[1]
then;
Axis of symmetry is given by:
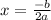
Vertex =
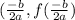
As per the statement:
The equation :
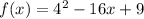
On comparing with [1] we have;
a = 4, b = -16 and c =9
we have;
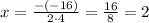
Substitute x= 2 in f(x) we have;
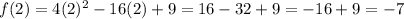
Vertex = (2, -7)
therefore, the vertex of the parabola is, (2, -7)