Question

Determine en donde la funcion dada es creciente,concava hacia riba y concava hacia abajo. y= x3–3x–1

Answer 1

Es creciente en los siguientes intervalos:
`[-\infty,-1] U [1,\infty]`

Es concavo hacia abajo en el intervalo:
`[-\infty,0)`

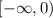
Es concavo hacia arriba en el intervalo:
`(0,\infty]`

Explanation:

Sea la función:

`f(x)=x^(3)-3x-1`

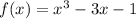
Para determinar el intervalo de crecimeinto debes determinar la primer derivada de la función (f'(x)). El intervalo donde f'(x) > 0 es creciente.

La derivada de f(x) es:

`f'(x)=3x^(2)-3`

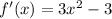
Entonces es creciente en los siguientes intervalos:

`[-\infty,-1] U [1,\infty]`

Ahora para determinar la concavidad debemos determinar la segunda derivada de la función (f''(x)). Si f''(x) > 0 la función es concava hacia arriba, si f''(x) < 0 la funcion es concava hacia abajo.

La segunda derivada de f(x) es:

`f''(x)=6x`

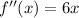
Por lo tanto:

Es concavo hacia abajo en el intervalo:
`[-\infty,0)`

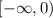
Es concavo hacia arriba en el intervalo:
`(0,\infty]`

Espero te haya ayudado!