Question

The equation tan(55 degree) equals StartFraction 15 Over b EndFraction can be used to find the length of Line segment A C.

Answer 1

Given:

The equation is

`\tan(55^\circ)=(15)/(b)`

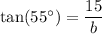
To find:

The length of the line segment AC.

Solution:

We have,

`\tan(55^\circ)=(15)/(b)`

`1.428148=(15)/(b)`

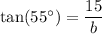
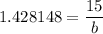
Multiply both sides by b.

`1.428148b=15`

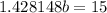
Divide both sides by 1.428148.

`b=(15)/(1.428148)`

`b=10.50311`

`b\approx 10.503`

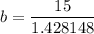
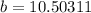
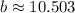
In a triangle ABC, the line of line segment AC is b. So,

`AC\approx 10.503`

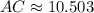
Therefore, the length of the line segment AC is 10.503 units.