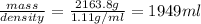Question

How many liters of the antifreeze ethylene glycol [CH2(OH)CH2(OH)] would you add to a car radiator containing 6.50 L of water if the coldest winter temperature in your area is -10.°C? (The density of ethylene glycol is 1.11 g/mL. Assume the density of water at -10.°C is 1.00 g/mL.)

Answer 1

16 = m x 1.86
m = 8.60 = moles solute / 6.50 Kg

moles solute = 55.9

mass solute = 55.9 x 62.068 g/mol=3470 g

V = 3479/ 1.11 =3126 mL= 3.13 L

delta T = 8.60 x 0.512 =4.40
boling point = 104.4 °C

Hope this helps.

Answer 2

Around 2.0 L of ethylene glycol needs to be added to the car radiator

Step-by-step explanation:

The depression in freezing point ΔTf of a solution is directly proportional to its molality (m), i.e.

`\Delta T_(f)= T_(f)^(0)-T_(f)=i*K_(f)*m`

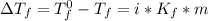
From the given information:

`T_(f)` = freezing pt of solution = -10.0 C

`T_(f)^(0)` = freezing pt of pure solvent = 0 C

Kf = freezing pt depression constant = 1.86 C/m

i = 1 for ethylene glycol antifreeze

`[0-(-10.0)] C= 1*(1.86 C/m) *( m)\\\\m = 5.38`

`Molality = (moles\ of\ solute)/(kg\ solvent) \\\\Therefore,\ moles of antifreeze = molality* mass\ of\ water\\`

`Molality = (moles\ of\ solute)/(kg\ solvent) \\\\Therefore,\ moles of ethylene glycol = molality* mass\ of\ water\\`

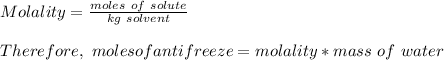
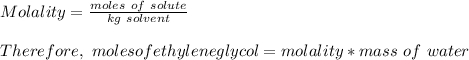
Volume of water = 6.50 L = 6500 ml

Density of water = 1.00 g/ml

Therefore mass of water =
`density * volume = 1.00g/ml*6500ml = 6500g = 6.50kg`

`moles\ of\ ethylene glycol= 5.38moles/kg*6.50kg = 34.9 moles`

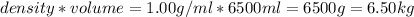
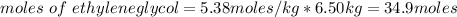
Molar mass of ethylene glycol = 62 g/mol

Mass of ethylene glycol needed =
`molar\ mass* moles = 62g/mol*34.9moles=2163.8g`

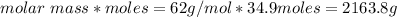
Density of ethylene = 1.11 g/ml

Therefore, volume needed =
`(mass)/(density) =(2163.8g)/(1.11g/ml) =1949ml`