Question

Binomial distribution formula with parameters regarding probability Final bike inspectionThe probability EXACTLY 4 out of 5 spots bikes will pass final bike inspectionThe probability LESS THAN 3 out of 5 sports bikes will pass final bike inspection. N=5 P=0.95I need step by step with factorial Ps and bionomal disbution get the sum and add together to find sum of each one please help

Answer 1

Given

A company makes Citi bikes. 95% pass final inspection.

Suppose that 5 bikes are randomly selected.

To find:

a) What is the probability that exactly 4 of these 5 bikes pass final inspection?

b) What is the probability that less than 3 out of 5 sports bikes pass final inspection?

Step-by-step explanation:

It is given that,

A company makes Citi bikes. 95% pass final inspection.

Suppose that 5 bikes are randomly selected.

That implies,

`\begin{gathered} n=5 \\ p=0.95 \\ q=1-p \\ =1-0.95 \\ =0.05 \end{gathered}`

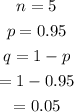
Then,

a) The probability that exactly 4 bikes pass the final inspection is,

`\begin{gathered} P(X=4)=5C_4*(0.95)^4*(0.05)^(5-4) \\ =(5!)/(4!(5-4)!)*0.8145*(0.05)^1 \\ =5*0.40725 \\ =0.2036 \end{gathered}`

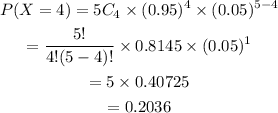
Hence, the probability that exactly 4 bikes pass the final inspection is 0.2036.

b) The probability that less than 3 bikes pass the final inspection is,

`\begin{gathered} P(X<3)=1-P(X\ge3) \\ =1-[P(X=3+P(X=4)+P(X=5)] \\ =1-[P(X=3)+0.2036+P(X=5)]\frac{}{} \end{gathered}`

Then,

`\begin{gathered} P(X=3)=(5!)/(3!(5-3)!)*(0.95)^3*(0.05)^(5-3) \\ =(5*4)/(2)*0.857375*(0.05)^2 \\ =10*0.002143 \\ =0.02143 \end{gathered}`

`\begin{gathered} P(X=5)=nC_5*(0.95)^5*(0.05)^(5-5) \\ =(5!)/(5!(5-5)!)*0.7738*(0.05)^0 \\ =0.7738 \end{gathered}`

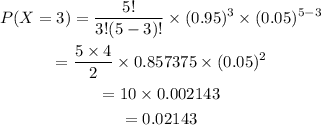
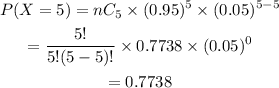
Then,

`\begin{gathered} P(X<3)=1-[0.02143+0.2036+0.7738] \\ =1-0.9988 \\ =0.0012 \end{gathered}`

Hence, the probability that less than 3 bikes will pass the final inspection is 0.0012.