for a) is just the distance formula
![\bf \textit{distance between 2 points}\\ \quad \\ \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) A&({{ x}}\quad ,&{{ 1}})\quad % (c,d) B&({{ -4}}\quad ,&{{ 1}}) \end{array}\qquad % distance value \begin{array}{llll} d = \sqrt{({{ x_2}}-{{ x_1}})^2 + ({{ y_2}}-{{ y_1}})^2} \\\\\\ √(8) = \sqrt{({{ -4}}-{{ x}})^2 + (1-1)^2} \end{array}]()
-----------------------------------------------------------------------------------------
for b) is also the distance formula, just different coordinates and distance
![\bf \textit{distance between 2 points}\\ \quad \\ \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) A&({{ -7}}\quad ,&{{ y}})\quad % (c,d) B&({{ -3}}\quad ,&{{ 4}}) \end{array}\ \ \begin{array}{llll} d = \sqrt{({{ x_2}}-{{ x_1}})^2 + ({{ y_2}}-{{ y_1}})^2} \\\\\\ 4√(2) = √((-3-(-7))^2+(4-y)^2) \end{array}]()
--------------------------------------------------------------------------
for c) well... we know AB = BC.... we do have the coordinates for A and B
so... find the distance for AB, that is
![\bf \textit{distance between 2 points}\\ \quad \\ \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) A&({{ -3}}\quad ,&{{ 0}})\quad % (c,d) B&({{ 5}}\quad ,&{{ -2}}) \end{array}\qquad % distance value \begin{array}{llll} d = \sqrt{({{ x_2}}-{{ x_1}})^2 + ({{ y_2}}-{{ y_1}})^2}\\\\ d=\boxed{?} \end{array}]()
now.. whatever that is, is = BC, so the distance for BC is
![\bf \textit{distance between 2 points}\\ \quad \\ \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) B&({{ 5}}\quad ,&{{ -2}})\quad % (c,d) C&({{ -13}}\quad ,&{{ y}}) \end{array}\qquad % distance value \begin{array}{llll} d = \sqrt{({{ x_2}}-{{ x_1}})^2 + ({{ y_2}}-{{ y_1}})^2}\\\\ d=BC\\\\ BC=\boxed{?} \end{array}]()
so... whatever distance you get for AB, set it equals to BC, BC will be in "y-terms" since the C point has a variable in its ordered points
so.. .solve AB = BC for "y"
------------------------------------------------------------------------------------
now d) we know M and N are equidistant to P, that simply means that P is the midpoint of the segment MN
so use the midpoint formula
![\bf \textit{middle point of 2 points }\\ \quad \\ \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) M&({{-2}}\quad ,&{{ 1}})\quad % (c,d) N&({{ x}}\quad ,&{{ 1}}) \end{array}\qquad % coordinates of midpoint \left(\cfrac{{{ x_2}} + {{ x_1}}}{2}\quad ,\quad \cfrac{{{ y_2}} + {{ y_1}}}{2} \right)=P \\\\\\]()
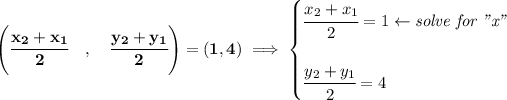
now, for d), you can also just use the distance formula, find the distance for MP, then since MP = PN, find the distance for PN in x-terms and then set it to equal to MP and solve for "x"