Question

A long-term bond returns you $21,171.63 at the end of ten years. Assuming an interest rate of 4.5% compounded daily, what was the amount of your initial investment?

Answer 1

`A=P(1+ (r)/(n))^(nt)`
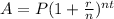
A=final amount
P=amount investeed
r=rate in decimal
n=number of times per year compounded

we need to solve for P
easy

`A=P(1+ (r)/(n))^(nt)`
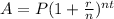
divide both sides by
`(1+ (r)/(n))^(nt)`

`(A)/((1+ (r)/(n))^(nt) ) =P`

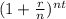
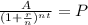
there are 365 or 366 days in a year depending on leap years (actually there are about 365.25 days per year so we jsut add 1 day every 4 years)

we will use 365 for number of days in a year

A=21171.63
P=P
r=4.5%=0.045
t=10
n=365


`(21171.63)/((1+ (0.045)/(365))^((365)(10)) ) =P`
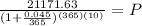
use your calculator
13500=P

initial investment was $13500

Answer 2

P=A/(1+i/m)^mn
P=21171.63/((1+0.045/360)^(360*10))
P=13,500.01