Question

What is the solution of √2x+4 -√x-2?

Answer 1

I hope this answer helped u

Answer 2

OK either the equation is
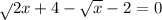
`\sqrt{} 2x+4 - √(x) -2 =0` or
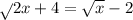
`\sqrt{} 2x+4 = √(x) -2` Either way it ends up the same because if it is the first equation, I would move the
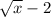
`√(x) - 2` to the other side of the equation. It would become
`√(x) + 2`.

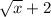
For my example, I am going with
`\sqrt{} 2x+4 = √(x) -2`
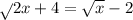
Square both sides
2x+4=
`(x+2)^(2)`
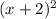
Then use FOIL to solve the right side
2x+4=
`x^(2) +2x+2x+4`
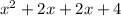
Then combine like terms
2x+4=
`x^(2) +4x+4`
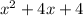
Set it equal to 0 and combine like terms

`0= x^(2) -2x`
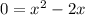
0=x(x-2)
So x=0 and x=2
If it was the other was it would be x=-2

Hope that helps.