We will have the following:
First, we find the equivalent of 15 & 9 ohms, that is:
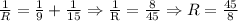
Then, we find the equivalent of R and 8 ohms:
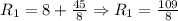
The, we find the equivalent of R1 and 25 ohms:
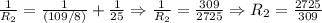
Finally, we calculate the equivalent of R2 and 10 ohms, that is:
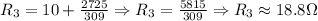
So, the equivalent resistance is approximately 18.8 ohms.