Question

Use the fact that the length of an arc intercepted by an angle is proportional to the radius to find the area of the sector given r = 3 cm and Θ =

π
4
.

Answer 1

sector area = (Central Angle (Degrees) / 360) * PI * radius^2
One way to solve this is that an angle of (PI/4) = 45 degrees.
45 degrees is one eighth of a circle.
Area of ENTIRE circle = PI*radius^2 = PI * 3^2 = 28.2743338823 square centimeters
Area of the sector is one eighth of this = 3.5342917353 square centimeters

Answer 2

Let l be the length of an ac and r be the radius of the circle.

Use the fact that the length of an arc intercepted by an angle is proportional to the radius

i.e

`l \propto r`

⇒
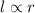
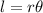`l = r \theta` where,
`\theta` is the angle in radian.

To find the Area of the sector:

Given: r = 3 cm and
`\theta = (\pi)/(4)`

`\text{Area of the sector A} = \pi r^2 \cdot (\theta)/(360^(\circ))`

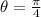
where,
`\theta` is the angle in degree.

Use conversion:

1 radian =
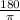`(180)/(\pi)` degree

then;

`(\pi)/(4)` =
`(\pi)/(4 ) * (180)/(\pi) = 45^(\circ)`

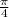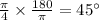
then;

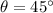`\theta =45^(\circ)` and use
`\pi = 3.14`

Substitute the given values we have;

`A= 3.14 \cdot 3^2 \cdot (45)/(360)`

⇒
`A = 3.14 \cdot 9 \cdot 0.125`

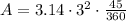
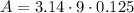
Simplify:

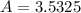`A = 3.5325` square cm

Therefore, the area of the sector is, 3.5325 square cm