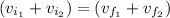Question

Two identical soccer balls are rolled towards each other. What will be true after they collide head-on

Answer 1

they will go away from each other

Answer 2

`(v_{i_(1) }+v_{i_(2) }) = (v_{f_(1) }+v_{f_(2) })`

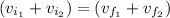
Step-by-step explanation:

There are some things we can say:

• If the Collision was Elastic, then the conservation of energy applies, where the kinetic energy of the system before they collide will be the same after they collide.
• If the collision was inelastic, then we can assert that the kinetic energy of the system before the collision and after the collision will be different, because there is some energy lost in the form of heat for example, though the energy of the entire system stays the same (if we add the losses).
• The law of conservation of momentum states that the momentum of the system before the collision is exactly the same after the collision so if
  `m_(1) =m_(2)`:

`m_{i_(1) } *v_{i_(1) }+m_{i_(2) } *v_{i_(2) } = m_{f_(1) } *v_{f_(1) }+m_{f_(2) } *v_{f_(2) }`

`m_{i_(1) } *(v_{i_(1) }+v_{i_(2) }) = m_{f_(1) } *(v_{f_(1) }+v_{f_(2) })`

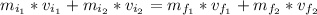
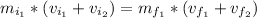
Since there is conservation of mass as well (we assume that nothing breaks apart after the collision):

`(v_{i_(1) }+v_{i_(2) }) = (v_{f_(1) }+v_{f_(2) })`