ANSWER
The quadratic function,

has no real roots.
Step-by-step explanation
We use the discriminant,
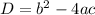
to determine the nature of the roots of a quadratic equation.
If we compare

to
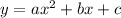
Then
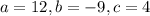
We substitute these values in to the formula for the discriminant, to obtain,
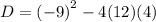
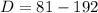
This implies that,
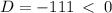
Since the discriminant is zero, the quadratic function,

has no real roots.