Question

For the image of the overhead projector to be in focus, the distance from the projector lens to the image, 
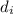
`d_(i)` , the projector lens focal length, f, and the distance from the transparency to the projector lens, 
`d_(0)` , must satisfy the thin lens equation
`(1)/(f)= (1)/( d_(i) )`+ 
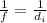
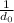
`(1)/( d_(0) )`. Which is the focal length of the projector lens if the transparency placed 4 inches from the projector lens is in focus on the screen, located 8 feet from the projector lens?

I'm especially unsure of what the last sentence means...

Answer 1

3.8in.

Step-by-step explanation:

Answer 2

Given:
distance from the projector lens to the image, di
projector lens focal length, f
distance from the transparency to the projector lens, do

thin lens equation: 1/f = 1/di + 1/do
do = 4 inches
di = 8 feet

convert feet to inches, for uniformity.
1 foot = 12 inches
8 feet * 12 inches/ft = 96 inches

1/f = 1/96 inches + 1/4 inches

Adding fractions, denominator must be the same.

1/f = (1/96 * 1/1) + (1/4 * 24/24)
1/f = 1/96 + 24/96
1/f = 25/96

to find the value of f, do cross multiplication
1*96 = f * 25
96 = 25f
96/25 = f
3.84 = f

The focal length of the project lens is 3.84 inches