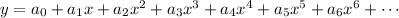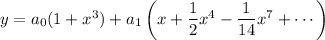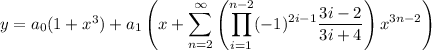Question

Power Series Differential equation

Given
`(x^3+1)y'' - 6xy =0`
a) use power series method to find general solution near x=0

I already got the recurrence equation of
`an+3= -an(n-3)/(n+3)`

i just need to know how to get the general solution

Answer 1

The next step is to solve the recurrence, but let's back up a bit. You should have found that the ODE in terms of the power series expansion for
`y`


`\displaystyle\sum_(n\ge2)\bigg((n-3)(n-2)a_n+(n+3)(n+2)a_(n+3)\bigg)x^(n+1)+2a_2+(6a_0-6a_3)x+(6a_1-12a_4)x^2=0`

which indeed gives the recurrence you found,


`a_(n+3)=-(n-3)/(n+3)a_n`

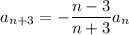
but in order to get anywhere with this, you need at least three initial conditions. The constant term tells you that
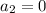
`a_2=0`, and substituting this into the recurrence, you find that
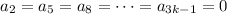
`a_2=a_5=a_8=\cdots=a_(3k-1)=0` for all
`k\ge1`.

Next, the linear term tells you that
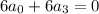
`6a_0+6a_3=0`, or
`a_3=a_0`.

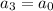
Now, if
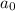
`a_0` is the first term in the sequence, then by the recurrence you have


`a_3=a_0`

`a_6=-(3-3)/(3+3)a_3=0`

`a_9=-(6-3)/(6+3)a_6=0`

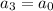
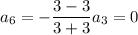
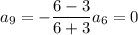
and so on, such that
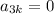
`a_(3k)=0` for all
`k\ge2`.

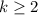
Finally, the quadratic term gives
`6a_1-12a_4=0`, or
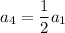
`a_4=\frac12a_1`. Then by the recurrence,


`a_4=\frac12a_1`

`a_7=-(4-3)/(4+3)a_4=\frac{(-1)^1}2\frac17a_1`

`a_(10)=-(7-3)/(7+3)a_7=\frac{(-1)^2}2\frac4{10*7}a_1`

`a_(13)=-(10-3)/(10+3)a_(10)=\frac{(-1)^3}2(7*4)/(13*10*7)a_1`

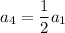
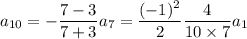
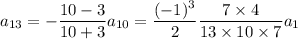
and so on, such that


`a_(3k-2)=\frac{a_1}2\displaystyle\prod_(i=1)^(k-2)(-1)^(2i-1)(3i-2)/(3i+4)`

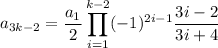
for all
`k\ge2`.

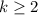
Now, the solution was proposed to be


`y=\displaystyle\sum_(n\ge0)a_nx^n`

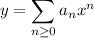
so the general solution would be


`y=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+\cdots`

`y=a_0(1+x^3)+a_1\left(x+\frac12x^4-\frac1{14}x^7+\cdots\right)`

`y=a_0(1+x^3)+a_1\displaystyle\left(x+\sum_(n=2)^\infty\left(\prod_(i=1)^(n-2)(-1)^(2i-1)(3i-2)/(3i+4)\right)x^(3n-2)\right)`