Answer:
D.
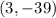
Explanation:
We have been given an equation
 . We are asked to find the vertex of parabola for our given equation.
. We are asked to find the vertex of parabola for our given equation.
We will use formula
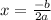 to find the x-coordinate of the vertex of parabola, then we will substitute the value of x-coordinate in our equation to find the y-coordinate of the parabola.
to find the x-coordinate of the vertex of parabola, then we will substitute the value of x-coordinate in our equation to find the y-coordinate of the parabola.

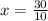
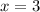
Therefore, the x-coordinate of the vertex of the parabola is 3.
Now let us substitute
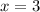 in our given equation to find the y-coordinate of the parabola.
in our given equation to find the y-coordinate of the parabola.
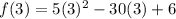
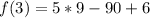
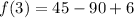
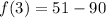
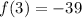
So, the y-coordinate of the vertex of parabola is
 . The point
. The point
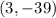 represents the vertex of the parabola represented by our given equation and option D is the correct choice.
represents the vertex of the parabola represented by our given equation and option D is the correct choice.