Question

A rectangular prism has a length of 2 1/2 cm, a width of 2 1/2 cm, and a height of 5 cm. Justin has a storage container for the prism that has a volume of 35 cm³. What is the difference between the volume of the prism and the volume of the storage container?

Answer 1

first calculate the volume of the rectangular prism, which is base area x height, 2.5x2.5x5 = 31.25
therefore the difference is 35 - 31.25= 3.75 cm3

Answer 2

The difference between the volume of the prism and the volume of the storage container is 35 - 31.25 = 3.75 cm³

Explanation:

Given : A rectangular prism has a length of
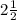`2(1)/(2)` cm, a width of
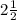`2(1)/(2)` cm, and a height of 5 cm.

Justin has a storage container for the prism that has a volume of 35 cm³.

We have to find the difference between the volume of the prism and the volume of the storage container.

Since the volume of the rectangular prism is given as the product of its length , width and height.

Mathematically written as,

Volume of rectangular prism = Length × Width × height

Given - length =
`2(1)/(2)=(5)/(2)` cm,

width =
`2(1)/(2)=(5)/(2)` cm,

and height = 5 cm.

Thus, Volume of rectangular prism =
`(5)/(2)* (5)/(2)* 5`

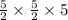
Simplify, we have,

Thus, Volume of rectangular prism =
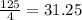`(125)/(4)=31.25` cm³

Thus, the difference between the volume of the prism and the volume of the storage container is 35 - 31.25 = 3.75 cm³