Answer:
The value of x is 66.
Explanation:
The median of a data set is the term that separates the lower half of the set from the upper half.
In a set with even cardinality, the median is given by the mean of it's two middle terms.
In this question:
Cardinality: 8
Middle terms: 4th and 5th, which are x - 5 and x + 1.
The median is 64.
This means that:
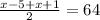
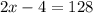
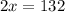
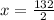
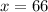
The value of x is 66.