Question

The length of an instant message conversation is normally distributed with a mean of 5 minutes and a standard deviation of 0.7 minutes. What is the probability that a conversation lasts longer than 6 minutes? 0.045 0.077 0.955 0.922

Answer 1

The probability of the message lasting longer than six minutes is 0.955. I hope this helps!

Answer 2

0.077

Explanation:

Data:

u = 5

σ = 0.7

x = 6

Calculation:

`P(X>x)=P(z>(x - u)/(devst))`

`P(X>6)=P(z>(6-5)/(0.7))`

`P(X>6)=P(z>(1)/(0.7))`

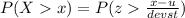
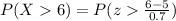
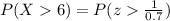
P (X> 6) = P [z> 1.43]

To find z> 1.43 in the normal distribution graph, we must subtract from the total probability (which is 1) the value of z <1.43 (note that the sign of inequality has been changed). So, we have

P (X> 6) = 1 - P [z <1.43]

We look in the normal distribution table for the z-score of 1.43, and get 0.92364. So,

P(X>6) = 1 - 0.92364

P(X>6) = 0.076564

P(X>6) = 0.077 (Rounded)

Hope this helps!