![\bf \begin{cases} f(x)=√(x+2)\\\\ g(x)=x^3-2 \end{cases}\qquad (g \circ f)(x)\iff g[\ f(x)\ ] \\\\\\ g[\ f(x)\ ]=\left( \boxed{f(x)} \right)^3-2\implies g[\ f(x)\ ]=\left( \boxed{√(x+2)} \right)^3-2 \\\\\\ g[\ f(x)\ ]=√((x+2)^3)-2\implies g[\ f(x)\ ]=(x+2)√(x+2)-2](https://img.qammunity.org/2018/formulas/mathematics/college/t0gvudo42pvobghh5x1g9n4tbvx6ul4l58.png)
now. the domain, will be constrained, by the issue that, an EVEN root, cannot have a negative radicand, so... theh square root, cannot have a negative amount inside.... so, "x" can have any real values, so long it doesn't make x+2 a negative number, now, 0 is ok, but less than that, no dice
let's see what makes x+2 to zero then
x+2 = 0 => x = -2
so if we set x = -2, we end up with (-2)+2 = 0, and that's ok for the domain
now, if we go below -2 though, like say (-3) + 2, then we end up with -1
if we make it -4, -5, -100 and so on, we end up with a negative radicand
so.... the domain will be
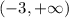
or x > -3