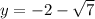Question

Find the value or values of y in the quadratic equation y2 + 4y + 4 = 7. A. y = −2 + √ 7 , y = −2 − √ 7 B. y = 2, y = 7 C. y = −2√ 7 , y = 2√ 7 D. y = 2 + 2√ 7 , y = 2 − 2√ 7

Answer 1

A) y = -2 + rt7, y = -2 - rt7

Answer 2

Option A

The values of y are:
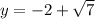`y=-2+√(7)` or
`y=-2-√(7)`.

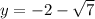Explanation:

`y^2+4y+4=7`

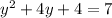
Subtract 7 from both the sides:

`y^2+4y+4-7=7-7`

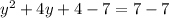
On Simplify:

`y^2+4y-3=0`

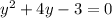
Solve with the quadratic formula:

For a quadratic equation of the form
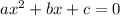`ax^2+bx+c=0` the solutions are:

`x_(1,2)=(-b\pm√(b^2-4ac))/(2a)`

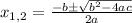
For a=1, b=4 and c=-3 we have,

`y_(1,2)=\frac{-4\pm √(4^2-4\cdot 1 \cdot (-3))} {2\cdot 1}`

`y_(1,2)=\frac{-4\pm√(16+12)} {2}`=
`\frac{-4\pm√(28)} {2}`

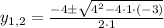
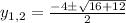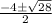
on solving we get,
`y_(1,2)=(-4\pm2√(7))/(2)`=
`-2\pm √(7)`

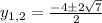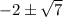
therefore, the values of y are:

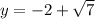`y=-2+√(7)` or
`y=-2-√(7)`