Answer:
Vertex of given quadratic function
 is (-2,-36)
is (-2,-36)
Explanation:
Given function

We have to find the vertex of the given function
 .
.
The standard quadratic function is represented by
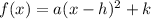 ,
,
Where (h,k) represents the vertex and a ≠ 0.
If a is positive, the graph opens upward, and if a is negative, then it opens downward.
We first write the given equation in standard form ,by using completing square,
We know

First taking 5 common from function, we have,

Comparing we have, a = x and
-2ab= +4x ⇒ -2b = 4 ⇒ b = -2
Add and subtract b
 , we get,
, we get,

On simplifying, we have,

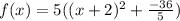
We get,

On comapring with standard equtaion , we have h = -2 and k = -36
Thus, vertex of given quadratic function
 is (-2 ,-36)
is (-2 ,-36)