Answer:
1. x = 6 cm
2. The coordinates of the x-intercept are (-15.798879, 0) and (8.177004, 0)
b) The maximum value of is y is approximately 459.874
The value of 'x' for which the maximum occurs is x is -3.8109375
c) 'k' is approximately -15.63748 or 'k' is approximately 8.0156
Explanation:
1. The area of rectangle ABCD - Area of triangle ABP = 114 cm²
Therefore, we have;
The area of rectangle ABCD = (2·x - 3)·(3·x + 1)
∴ The area of rectangle ABCD = 6·x² + 2·x - 9·x - 3 = 6·x² - 7·x - 3
The area of triangle ABP = 1/2 × (3·x + 1)·x = 3·x²/2 + x/2
The area of rectangle ABCD - Area of triangle ABP = 6·x² - 7·x - 3 - 3·x²/2 - x/2
6·x² - 7·x - 3 - 3·x²/2 + x/2 = 9·x²/2 - 13·x/2 - 3 = 114
9·x²/2 - 15·x/2 - 3 = 114
9·x² - 15·x - 6 - 228 = 0
9·x² - 15·x - 234 = 0
x = (15 ± √((-15)² - 4 × 9 × (-234)))/(2 × 9) = (15 ± 93)/18
∴ x = 6 or x = -13/3
Given that x is a natural number, we have that x = 6 cm
2. The given equation is 'y = -3.2·x² - 24.39·x + 413.4'
Therefore, we have;
The x-intercept are the values of 'x', where the value of 'y' is 0
Therefore, we have, at the x-intercept;
y = 0 = -3.2·x² - 24.39·x + 413.4
By the quadratic formula, we have;
x = (24.39 ± (√((-24.39)² - 4×(-3.2)×413.4)))/(2 × (-3.2))
x ≈ -15.798879 or x ≈ 8.177004
The coordinates of the x-intercept are;
(-15.798879, 0) and (8.177004, 0)
b) The maximum is given at dy/dx = 0
Therefore, at the maximum point, we have;
dy/dx = d(-3.2·x² - 24.39·x + 413.4)/dx = -6.4·x - 24.39 = 0
dy/dx = -6.4·x - 24.39 = 0
∴ x = 24.39/(-6.4) = -3.8109375
x = -3.8109375 at the maximum point
At the maximum point, we have;
y = -3.2·x² - 24.39·x + 413.4 = -3.2·(-3.8109375)² - 24.39·(-3.8109375) + 413.4 ≈ 459.874
y ≈ 459.874
Therefore, the maximum value of 'y' is given as follows
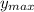≈ 459.874
The value of 'x' for which the maximum occurs is x = -3.8109375
c) The coordinate of the point is (12.3, k), therefore, we have;
y = -3.2·x² - 24.39·x + 413.4
When y = 12.3, therefore, -3.2·x² - 24.39·x + 413.4 = 12.3
-3.2·x² - 24.39·x + 413.4 = 12.3
-3.2·x² - 24.39·x + 413.4 - 12.3 = -3.2·x² - 24.39·x + 401.1 = 0
By the quadratic formula, we have;
x = (24.39 ± √((-24.39)² - 4×(-3.2)×401.1))/(2 × (-3.2))
x ≈ -15.63748 or x ≈ 8.015600
Therefore, k ≈ -15.63748 or k ≈ 8.015600