Answer:
The length of the base is 12 m
Explanation:
Given : The height of a triangle is 5 m less than its base. The area of the triangle is 42 m².
We have to find the length of the base.
Given the height of triangle is 5 m less than base
Let base be x then height is ( x -5 ) m
Area of triangle is
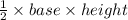
also given area of triangle is 42 m²
substitute, we get,
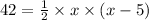
Solving , we get,
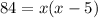
Simplify we get a quadratic equation as,

Using quadratic formula,
For the standard quadratic equation
 , the solution of roots is given by,
, the solution of roots is given by,
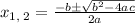
For a = 1 , b= -5 , c = -84 , we get
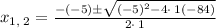
Simplify, we get
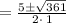
We know
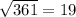 , we get
, we get

 and
and
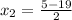
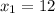 and
and

ignoring negative value as side cannot be negative.
thus, x = 12
base is 12 m then height is ( 12 -5 ) m = 4 m
Thus, the length of the base is 12 m.