Question

Find any points of discontinuity for the rational function. y=x-5/x^2-7x-8

Answer 1

The function is not continuous at x= -1 and x= 8

Explanation:

The given function is,

`y=(x-5)/(x^2-7x-8)`

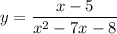
Factoring the denominator,

`=x^2-7x-8`

`=x^2-8x+x-8`

`=x(x-8)+1(x-8)`

`=(x+1)(x-8)`

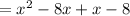
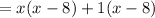
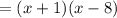
Now the function becomes,

`y=(x-5)/((x+1)(x-8))`

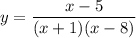
The function is not defined (it does not exist) for x= -1 and for x= 8, because the denominator is zero for those values of x.

To be continuous, the function has to be defined. So at those points the function is not continuous.

*At x= -1 and at x= 8 , the function has a vertical asymptote.

Answer 2

For discontinuity of the function:
x² - 7 x - 8 ≠ 0
x² - 8 x + x - 8 = 0
x ( x - 8 ) + ( x - 8 ) ≠ 0
( x - 8 ) ( x + 1 ) ≠ 0
The points of discontinuity are: x = - 1 and x = 8.
As for the Domain of the function:
x ∈ ( - ∞, - 1 ) ∪ ( - 1 , 8 ) ∪ ( 8, +∞ ).