Answer:
(10,1)
Explanation:
Let No. of iced tea be x
Let no. of lemonades be y
We are given that You need to purchase at least 9 gallons of drinks
So, equation becomes:
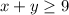 --1
--1
Cost of 1 gallon of ice tea = $4
Cost of x gallons of ice tea = $4x
Cost of 1 gallon of lemonade = $6
Cost of y gallons of lemonade = $6y
We are also given that you have at most $55 to spend.
So, equation becomes:
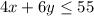 ---2
---2
Now Check the given points which satisfies the inequalities
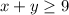 and
and
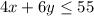
At (10,10)
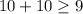 and
and
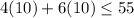
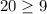 and
and

(10,10) is not satisfying the both equations
At (10,-5)
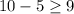 and
and
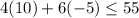
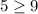 and
and

(10,-5) is not satisfying the both equations
At (2,10)
 and
and

 and
and
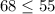
(2,10) is not satisfying the both equations.
At (10,1)
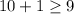 and
and

 and
and
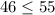
(10,1) is satisfying the both equations.
Thus (10,1) is a possible solution to the system of inequalities